√ f(x) math graph 167775-F(x y) function graph

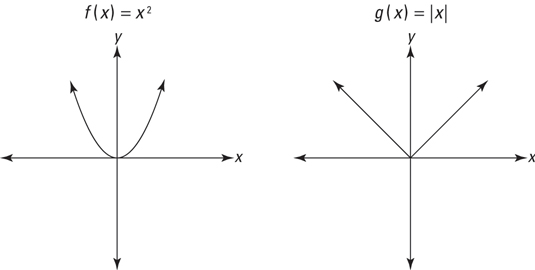
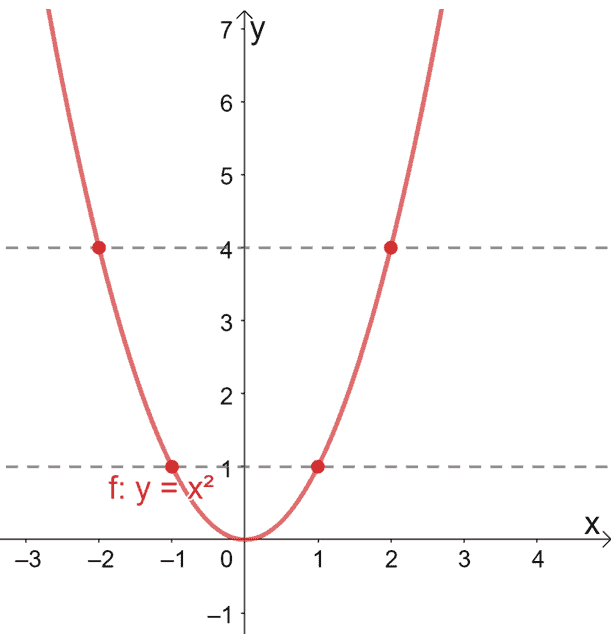
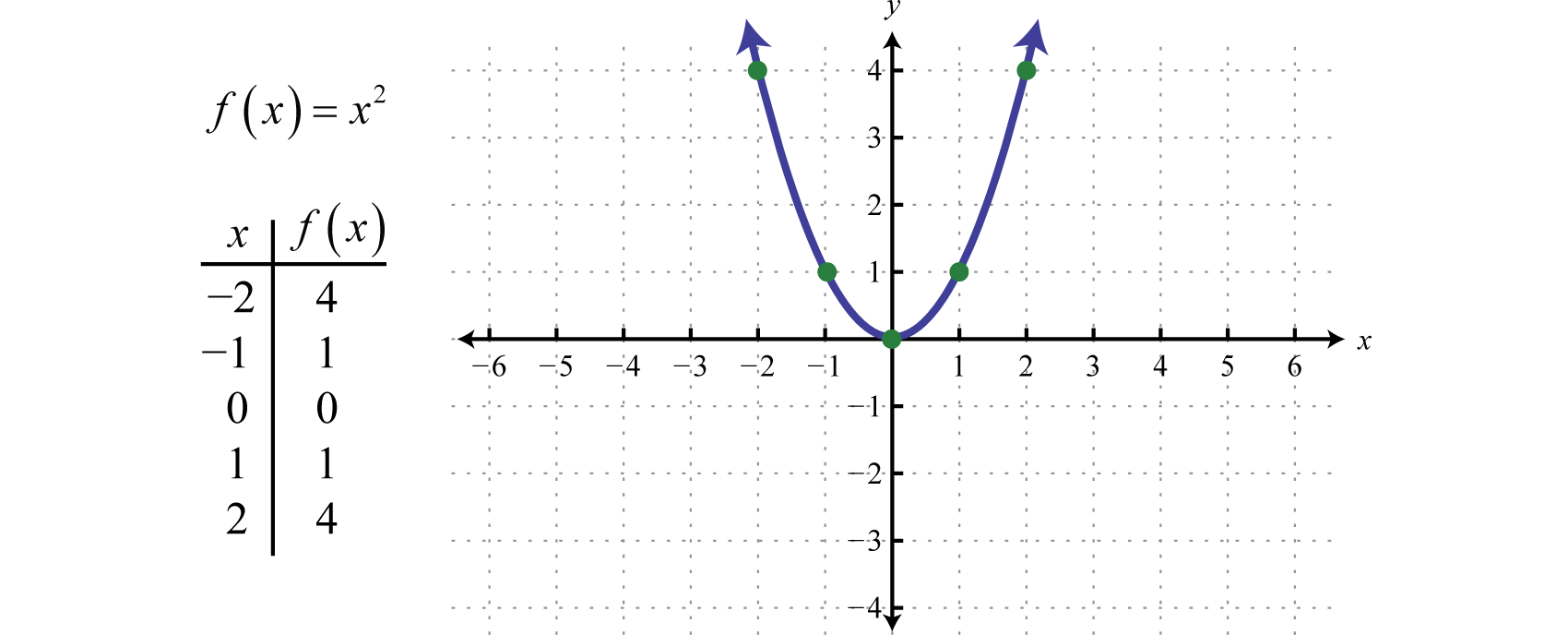
From to Connect Dotted Dashed – Dashed — Fill in Fill out Show term Second graph g (x) Derivative Integral C Blue 1 Blue 2 Blue 3 Blue 4 Blue 5 Blue 6 Red 1 Red 2 Red 3 Red 4 Yellow 1 Yellow 2 Green 1 Green 2 Green 3 Green 4 Green 5 Green 6 Black Grey 1 Grey 2 Grey 3 Grey 4 White Orange Turquoise Violet 1 Violet 2 Violet 3 Violet 4Math Functions 13 f(x) 2{x}2 3 (X) 1, xel1, 1), where () denotes the tra 14 f(x) 1 where denotes the greatest integer function, Il X21 15 If a function is defined, as g(x) sin x sin x, 6(x) = sin x cos x,0 sx 5m, then find The graph of #f(x)=x^2# is called a "Parabola" It looks like this One of the ways to graph this is to use plug in a few xvalues and get an idea of the shape Since the x values keep getting squared, there is an exponential increase on either side of the yaxis

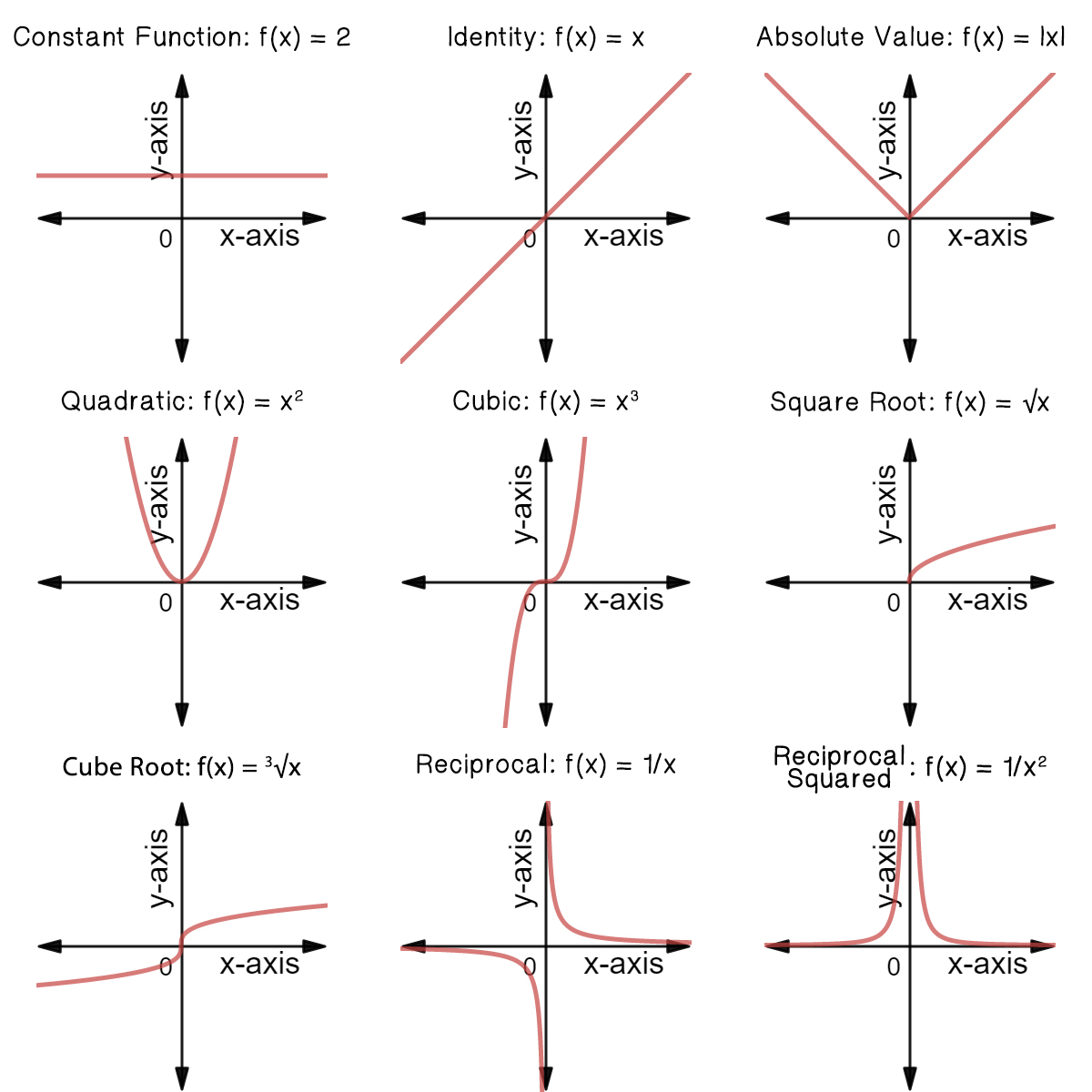
Classifying Common Functions Expii

F(x y) function graph

F(x y) function graph-When you want a quick graph of a function, you can just go to http//graphsketchcom/ function, like http//graphsketchcom/sin (x) You can even separate multiple equations with commas, like http//graphsketchcom/sin (x),x^2 For more information on GraphSketch (how it works, etc), see my blog post on itLinear functions have the form f(x) = ax b, where a and b are constants In Figure 111, we see examples of linear functions when a is positive, negative, and zero Note that if a > 0, the graph of the line rises as x increases In other words, f(x) = ax b is increasing on ( − ∞, ∞)

Which Is The Graph Of F X 5 2 X Learn Lif Co Id

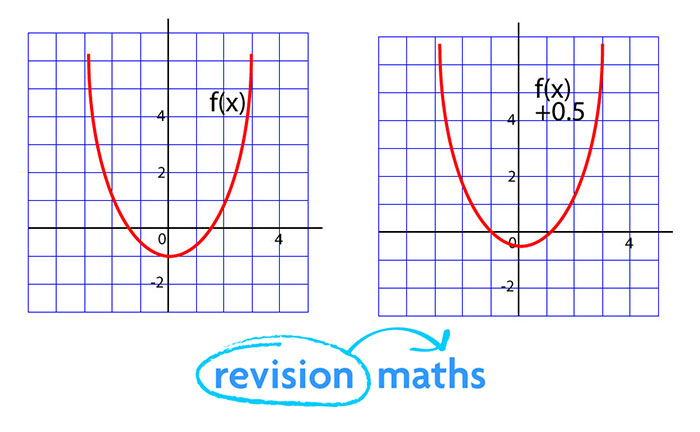
Graph of y = f(x) k Adding or subtracting a constant \(k\) to a function has the effect of shifting the graph up or down vertically by \(k\) units Graph of y = f(x)Let me take a look You'll be able to enter mathF X Math Graph feed and grow fish prognathodon location fear the walking dead season 6 episode 8 release date feed and grow fish megalodon location fear the walking dead season 5 blu ray release date fear the walking dead season 6 episode 8 spoilers fear the walking dead season 5 episode 15 cast fear the walking dead season 6 episode 2 free

The graph of h(x) can be identified as the only growing exponential function with a vertical intercept at (0,4) The graphs of f ( x ) and g ( x ) both have a vertical intercept at (0,2), but since g ( x ) has a larger growth factor, we can identify it as the graph increasing faster Find the intercepts and asymptotes, plot a few points, and then sketch the graph f(x)=4^x Step 1 Find the domain and range f(x) is defined for all real values of x, so the domain is the set of all real numbers 4^x>0, so the range is f(x)>0 Step 2 Find the yintercept Let x=0 y= 4^0 = 1 The yintercept is at (0,1) Step 3 Find the xintercept The dotted graph is f(2x), compressed (shrunk) by a factor of 1/2 horizontally;

The graph of 2 f (x) 2f(x) 2 f (x) is the graph of f (x) f(x) f (x) stretched vertically by a factor of 2 In a similar manner, we can see that to stretch a function vertically by c c c, we multiply on the outside of the function c f (x) cf(x) c f (x) is the graph of f (x) f(x) f (xYou can us the simple idea to draw the graph f(x) > $\infty$ ∞ , y=1/f(x) > 0;Thus, the graph of $\,y=3f(x)\,$ is found by taking the graph of $\,y=f(x)\,$, and multiplying the $\,y$values by $\,3\,$ This moves the points farther from the $\,x$axis, which tends to make the graph

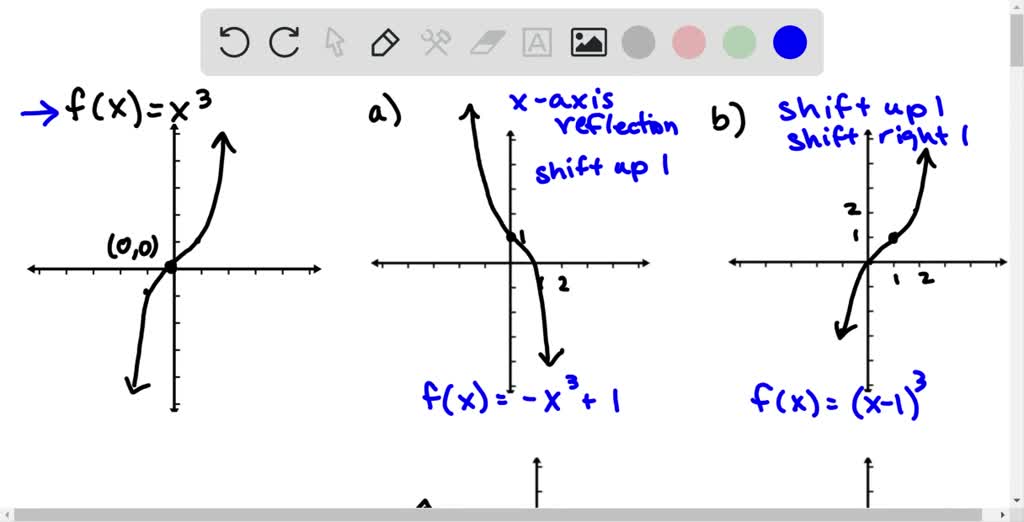
Solved Use The Graph Of F X X 3 To Write An Equation For Each Function Whose Graph Is Shown

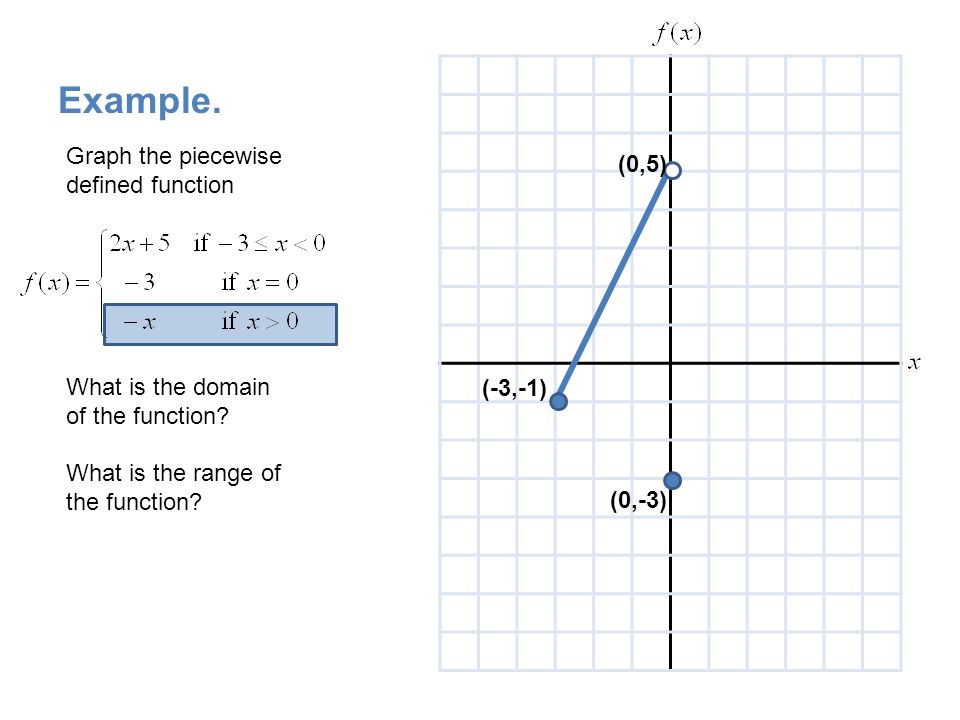
Graphing Piecewise Functions Ppt Download

 b) if f(x) is constant or reach to an extremum, f '(x) = 0, which means the graph of y = f '(x) falls on the xaxis;About Math Insight log in Image Graph of $f(x)=x^24$ Image file graph_x_squared_minus_4png Image links This image is found in the pages Solving single autonomous differential equations using graphical methods List of all imagesThe graph of $f(x)$ is the mirror image of the graph of $f(x)$ with respect to the horizontal axis A function is called even if $f(x)=f(x)$ for all $x$ (For example, $\cos(x)$) A function is called odd if $f(x)=f(x)$ for all $x$ (For example, $\sin(x)$)

Question 1 Sketching The Gradient Of A Given Graph From Left To Right Download Scientific Diagram

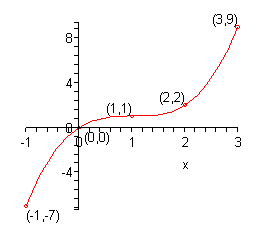
Algebra Graphing Functions

This means that the graph rapidly decreases towards 0 as x increases Below is a graph of f(x) = 2 x For values of the base between 0 and 1, such as f(x) = 03 x , the graph of the exponential function also approaches 0 as x approaches infinity F(x) = f(x) − k Table 251 Example 251 Sketch the graph of g(x) = √x 4 Solution Begin with the basic function defined by f(x) = √x and shift the graph up 4 units Answer Figure 253 A horizontal translation 60 is a rigid transformation that shifts a graph left or right relative to the original graph4321 0 1 2 3 44 3 2 1 0 1 2 3 4 The graphs of f(x) = sinx, and y = x,y = x− x3 6, y = x− x3 6 x5 1,y = x− x3 6 x5 1 − x7 5040

Operations On Functions Translations Sparknotes

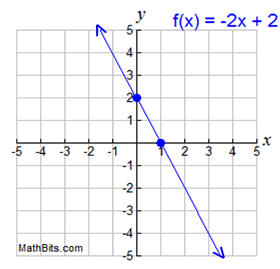
Features Of Function Graphs Mathbitsnotebook A1 Ccss Math

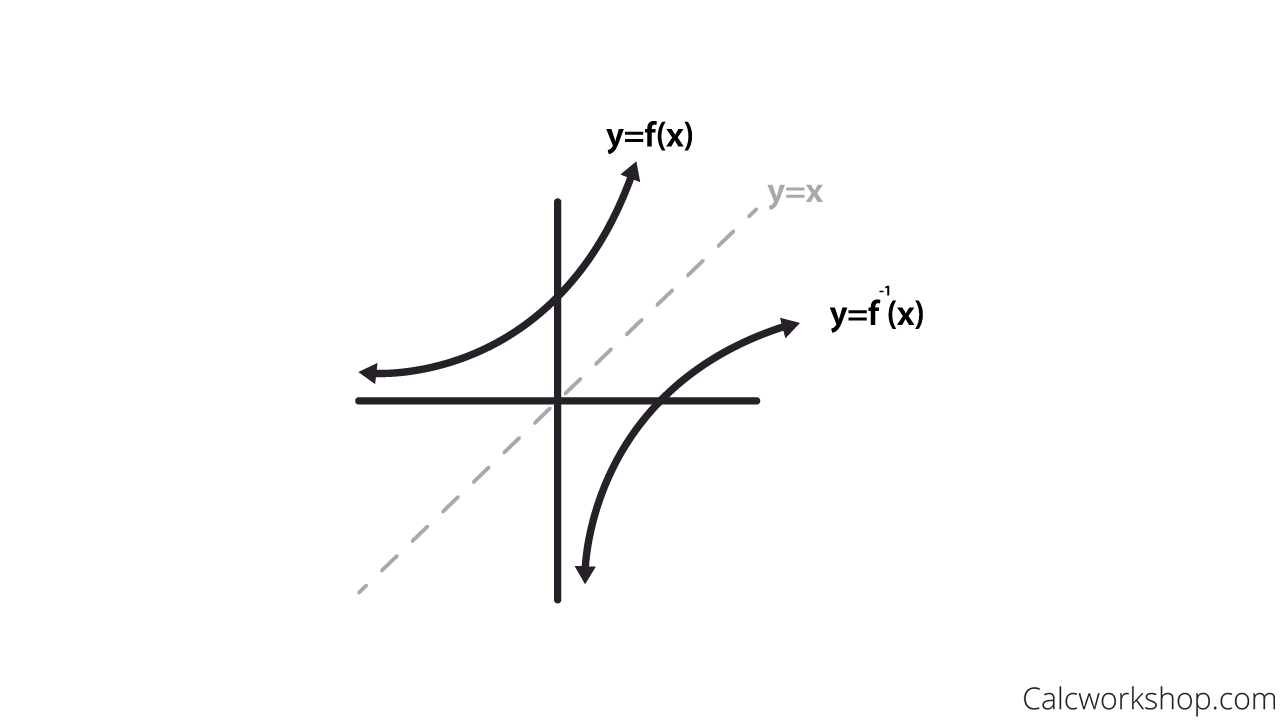
You can sketch the graph of f(x) using the information you have You know that at x = 1, 6, 8 the graph of f(x) has a horizontal tangent line So, all up and down the vertical lines x =1, x = 6, x = 8, draw short horizontal line segmentsthese are the tangent lines You know that at x= 5, the graph of f(x) has a tangent line with slope 3F1 (x) is the standard notation for the inverse of f(x) The inverse is said to exist if and only there is a function f1 with ff1 (x) = f1 f(x) = x Note that the graph of f1 will be the reflection of f in the line y = x This video explains more about the inverse of a functionExamples line\ (2,\4),\ (1,\2) slope\3x3y6=0 parallel\2x3y=9,\ (4,1) perpendicular\y=4x6,\ (8,26) domain\y=\frac {x^2x1} {x} range\y=\frac {x^2x1} {x} asymptotes\y=\frac {x} {x^26x8} extreme\points\y=\frac {x^2x1} {x}

1

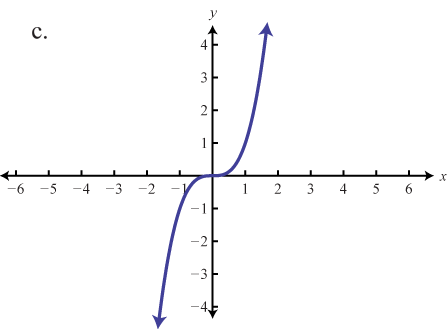
Graphing The Basic Functions

A math reflection flips a graph over the yaxis, and is of the form y = f (x) Other important transformations include vertical shifts, horizontal shifts and horizontal compression Let's talk about reflections Now recall how to reflect the graph y=f of x across the x axisMathf(x)=x/math Function is giving the absolute value of mathx/math whether mathx/math is positive or negative See the y axis of graph which is mathf(x)/math against mathx/math, as x axis It shows y axis values or mathf(xMath F SectionWorksheet Spring Sketch the graph of f(x) = x by plotting points at x = −,−,,, Sketch the graph of f(x) = x and g(x) = x on the same axes for − ≤ x

Function Graph F X Asin Bx C D Download Scientific Diagram

Functions Inverse And Composite Functions

First, go to the point P (x3, f(x3)) P ( x 3, f ( x 3)) on the graph of y = f(x) y = f ( x) This point has the y y value that we want, but it has the wrong x x value Move this point 3 3 units to the left Thus, the y y value stays the same, but the x x value is decreased by 3 3Here is how this function looks on a graph with an xextent of 10, 10 and a yextent of 10, 10 First, notice the x and yaxes They are drawn in red The function, f (x) = 1 / x, is drawn in green Also, notice the slight flaw in graphing technology which is usually seen when drawing graphs of rational functions with computers or The tangent line is just the line itself So f' would just be a horizontal line For instance, if f (x) = 5x 1, then the slope is just 5 everywhere, so f' (x) = 5 Then f'' (x) is the slope of a horizontal linewhich is 0 So f'' (x) = 0 See if you can guess

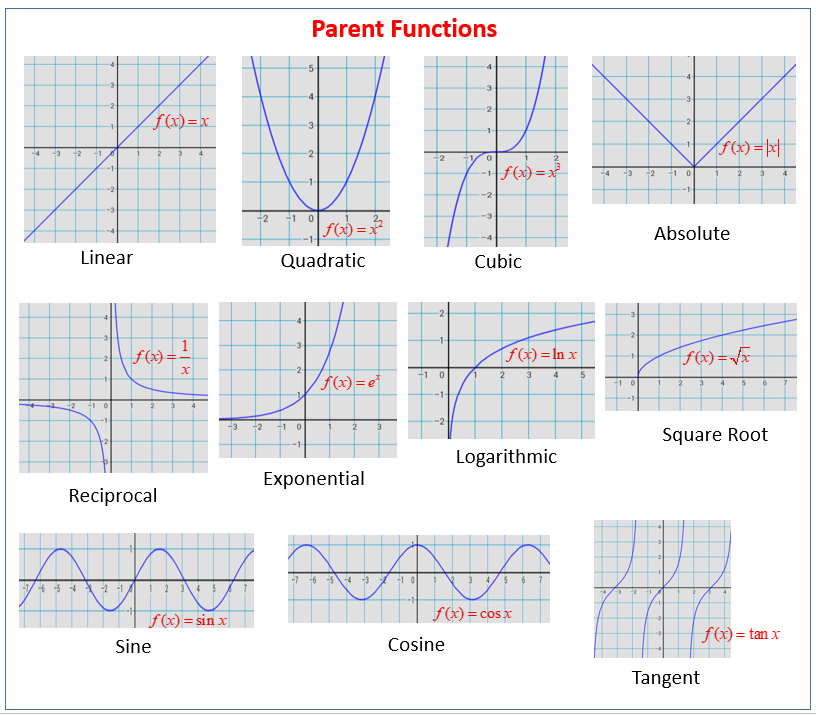
Parent Functions And Their Graphs Video Lessons Examples And Solutions

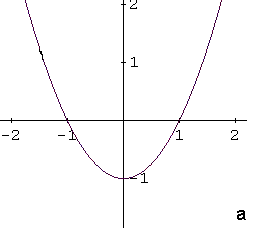
Identify Graphs Of Functions Tutorials

F ( 2) = 2 7 = 9 A function is linear if it can be defined by f ( x) = m x b f (x) is the value of the function m is the slope of the line b is the value of the function when x equals zero or the ycoordinate of the point where the line crosses the yaxis in the coordinate plane x is the value of the xcoordinateUnlock StepbyStep Graph f (x)=ln (x) Extended Keyboard ExamplesExplore math with our beautiful, free online graphing calculator Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more

Q Tbn And9gcsmm4ktmxrxm10kmsg3wqo5rzire Ogwbm0v2tajixhbesgniod Usqp Cau

Product Of Linear Functions

Every point of f has a corresponding image in f' Some useful reflections of y = f(x) are (i) The graph y = −f(x) is the reflection of the graph of f about the xaxis (ii) The graph y = f(−x) is the reflection of the graph of f about the yaxis (iii) The graph of y = f −1 (x) is the reflection of the graph of f in y = x TranslationLet us start with a function, in this case it is f(x) = x 2, but it could be anything f(x) = x 2 Here are some simple things we can do to move or scale it on the graph We can move it up or down by adding a constant to the yvalue g(x) = x 2 C Note to move the line down, we use a negative value for C C > 0 moves it up;By $f(x) = x^2 4$ I am telling you that if you input a number $x$ to this function then the function squares $x,$ subtracts 4 and returns the result Thus for example if $x = 3$ then $y = f(3) = 3^2 4 = 9 4 = 5$ To graph this function I would start by choosing some values of $x$ and since I get to choose I would select values that make the arithmetic easy

Operations With Functions Addition And Subtraction Of Functions Sparknotes

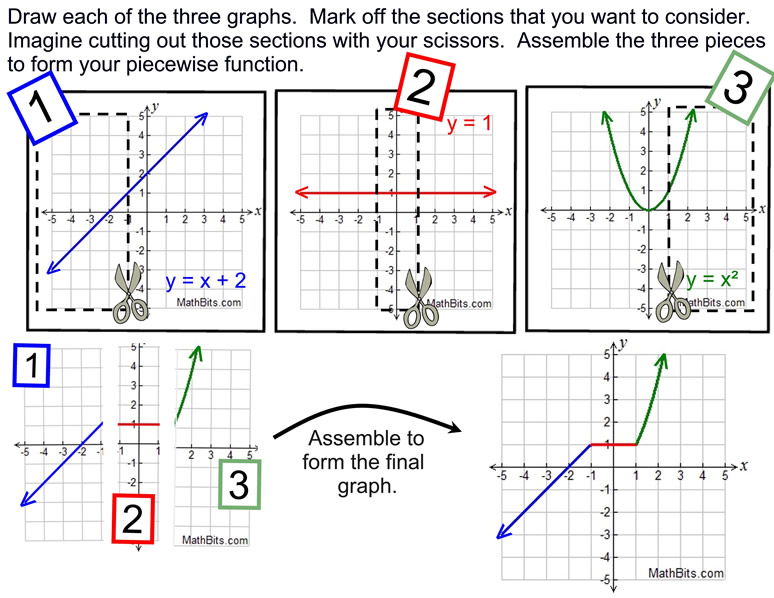
Piecewise Absolute Value And Step Functions Mathbitsnotebook A1 Ccss Math

Math Functions 13 f(x) 2{x}2 3 (X) 1, xel1, 1), where () denotes the tra 14 f(x) 1 where denotes the greatest integer function, Il X21 15 If a function is defined, as g(x) sin x sin x, 6(x) = sin x cos x,0 sx 5m, then findThe point (2, 4) moves to (4, 4), doubling x I first looked at the more natural vertical transformations from a new perspectiveThe graph of f(x) in this example is the graph of y = x 2 3 It is easy to generate points on the graph Choose a value for the first coordinate, then evaluate f at that number to find the second coordinate The following table shows several values for x and the function f

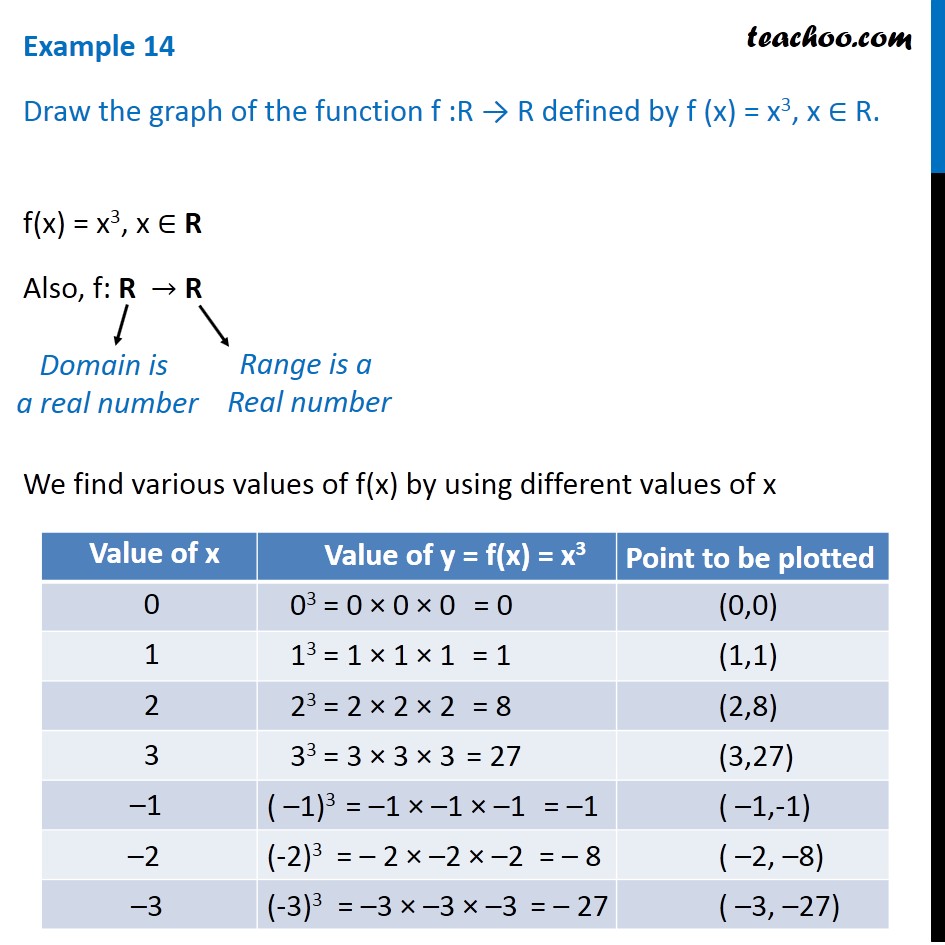
Example 14 Draw Graph Of F X X 3 Chapter 2 Class 11

Which Is The Graph Of F X 5 2 X Learn Lif Co Id

F(x) (a,b) 7!(a,b) flip over the xaxis Examples • The graph of f(x)=x2 is a graph that we know how to draw It's drawn on page 59 We can use this graph that we know and the chart above to draw f(x)2, f(x) 2, 2f(x), 1 2f(x), and f(x) Or to write the previous five functions without the name of the function f, these are the five functions x22,x22,Basic Math PreAlgebra Algebra Trigonometry Precalculus Calculus Statistics Finite Math Linear Algebra Chemistry Graphing Upgrade Examples About Help Sign In Sign Up Hope that helps!C) if f(x) is decreasing, f '(x) < 0, which means the graph of y = f '(x) falls below the xaxis If you wish try out your understanding towards the concept above, perhaps you can ask your friend's help to give you a graph of any

Function Definition Types Examples Facts Britannica

Graphing Functions With Excel

22ffx 2 − 2f − f x View solution steps Solution Steps g ( x ) = f ( x 2 ) 2 g ( x) = − f ( x 2) 2 Use the distributive property to multiply f by x2 Use the distributive property to multiply − f by x 2 \left (f\right)x2\left (f\right)2Properties depend on value of "a" When a=1, the graph is a horizontal line at y=1 Apart from that there are two cases to look at a between 0 and 1 Example f (x) = (05)x For a between 0 and 1 As x increases, f (x) heads to 0 As x decreases, f (x) heads to infinityI assume you know how to graph For each value of x the point on f (x) = x^2 4 is 4 units below the point with the same x value on g (x) = x^2 so take the graph of g (x) and move it down 4 units to obtain the graph of f (x) I'm confused by second part of your question I

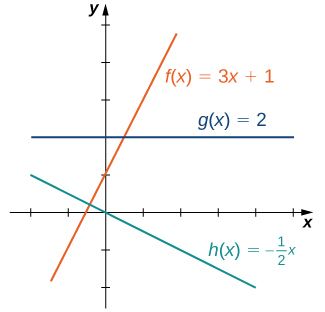
1 1 Functions And Their Graphs Mathematics Libretexts

How To Interpret Function Graphs Dummies

The symbol f(x), which is often used to name an algebraic expression in the variable x, can also be used to denote the value of the expression for specific values of x For example, if f(x) = 2x 4 where f{x) is playing the same role as y in Equation (2) on page 285, then f(1) represents the value of the expression 2x 4 when x is Use a graph of f(x) to determine the value of f(n), where n is a specific xvalueTable of Contents0000 Finding the value of f(2) from a graph of f(x)002F(x) > 0, y=1/f(x) > $\infty$ ∞ and the relation of f(x) and 1/f(x)

1

1

Graph f (x)= x MathwayC < 0 moves it down We can move it left or right by adding aThe point (2, 4) moves to (1, 4), halving the value of x The dashed graph is f(x/2), stretched by a factor of 2 horizontally;

What S The Graph Of Math F X X 2 X 2 Math Quora

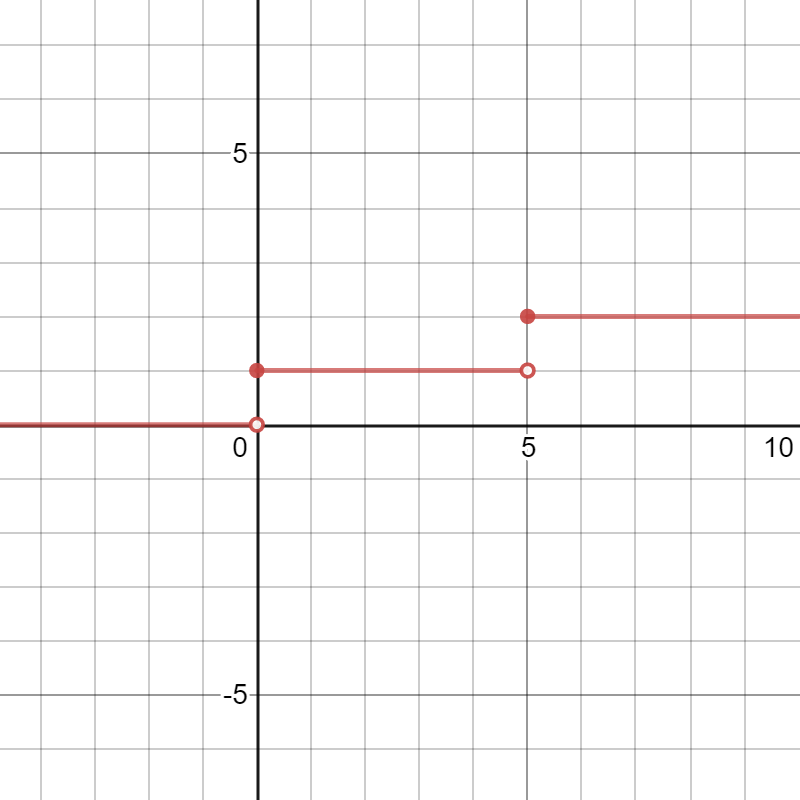
Step Functions Expii

Graphing Linear Function Type 1 Level 2 These pdf worksheets provide ample practice in plotting the graph of linear functions The slopes are represented as fractions in the level 2 worksheets For the given xcoordinates, find f (x) and complete the function tables Plot the points and graph

Surfaces As Graphs Of Functions Math Insight

Describing The Graph Of A Function

How To Graph And Find Inverse Functions 19 Terrific Examples

One To One Function Explanation Examples

Notes On Functions And Their Graphs Cbse Class 11 Maths

Graphing The Basic Functions

Graph Of A Function Wikipedia

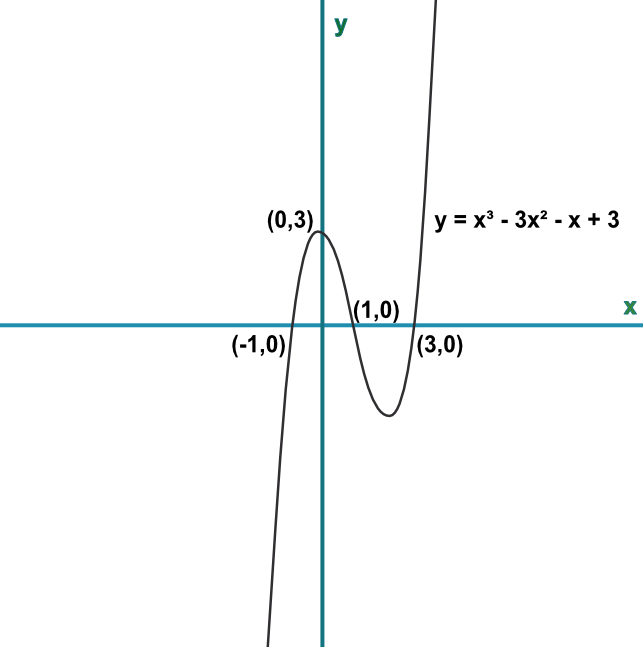
Graphing Cubic Functions

Classifying Common Functions Expii

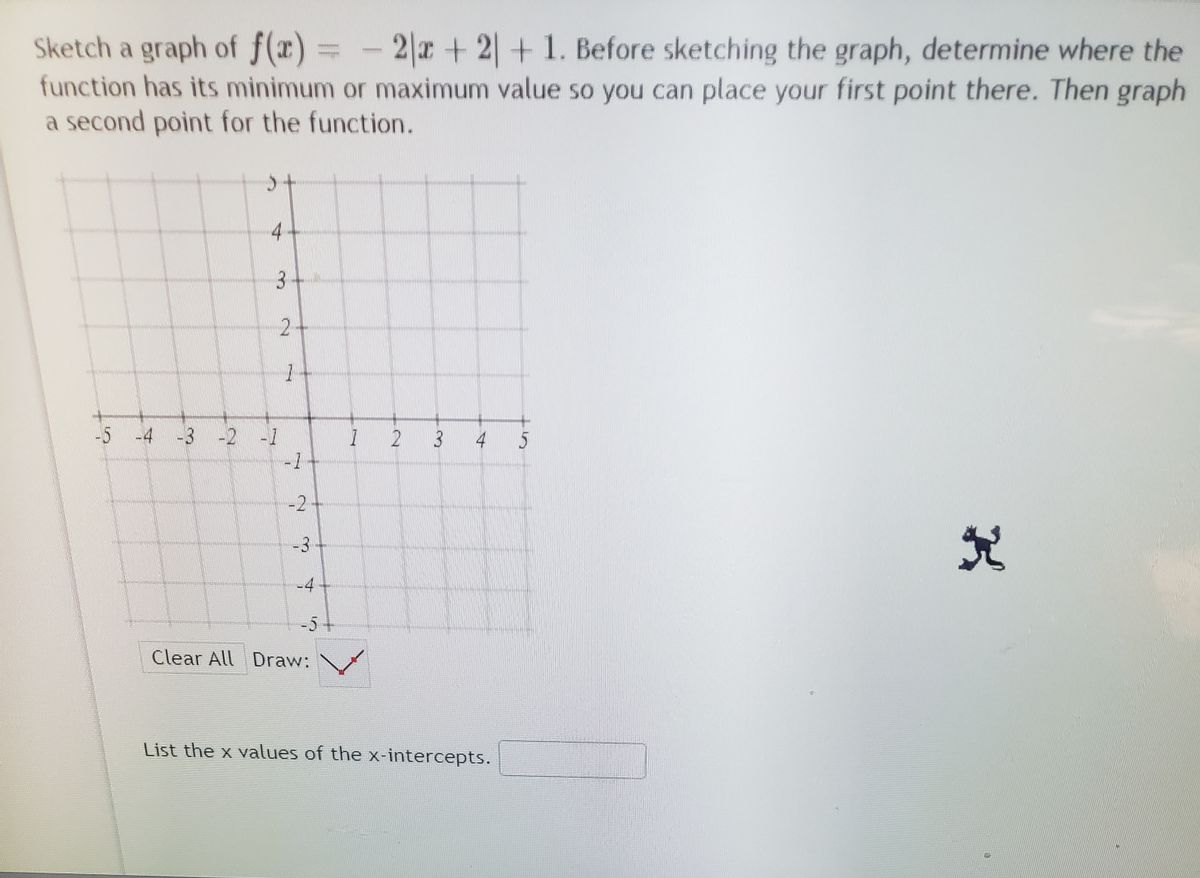
Answered Sketch A Graph Of F X Function Has Bartleby

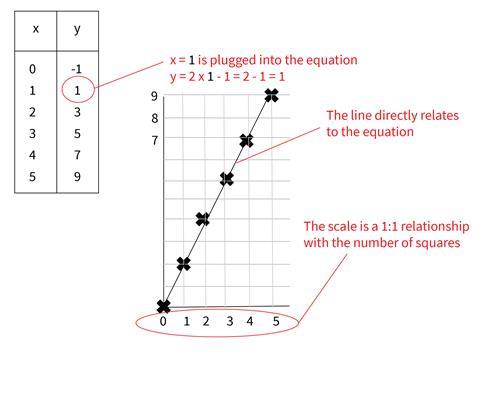
How To Approach Graphs In Chemistry Maths Rsc Education

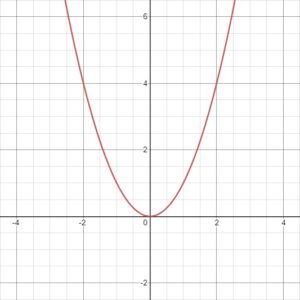
Domain And Range Of A Quadratic Function Video Practice

Pplato Flap Math 1 3 Functions And Graphs

Graphs Of Functions

Function Graphs

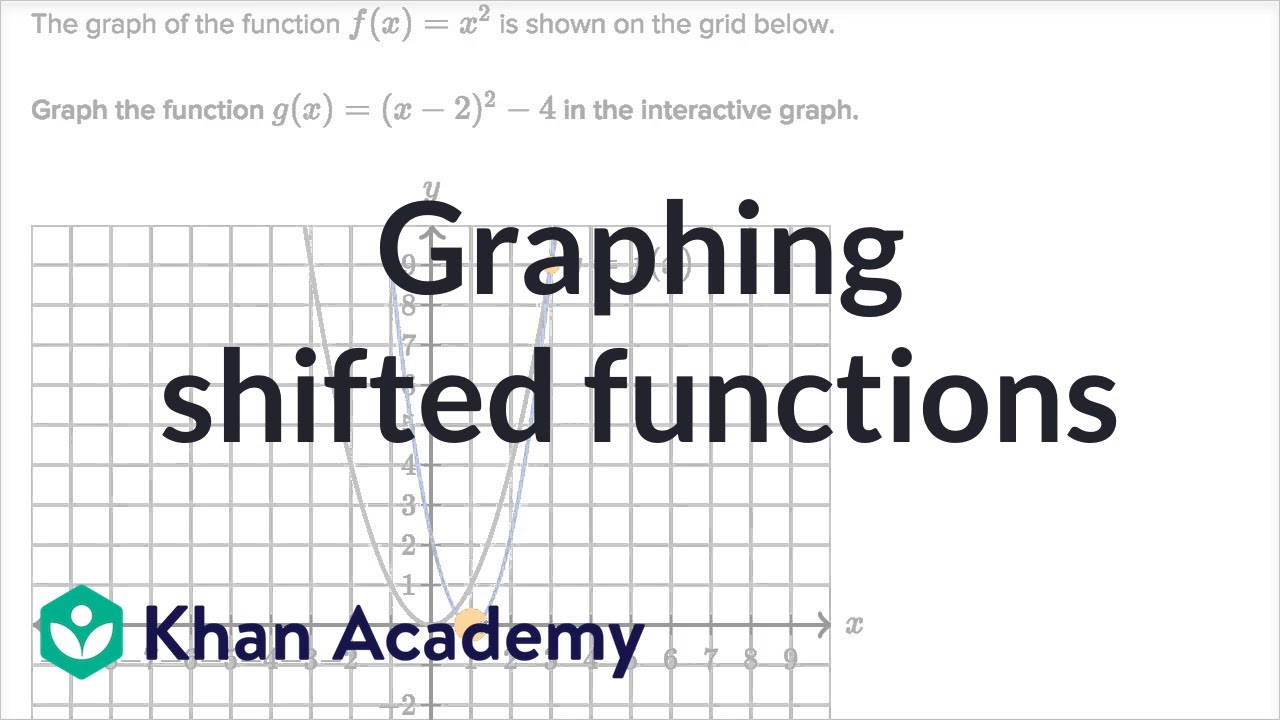
Graphing Shifted Functions Mathematics Iii High School Math Khan Academy Youtube

Graphs Of Functions

Reflecting Functions Examples Video Khan Academy

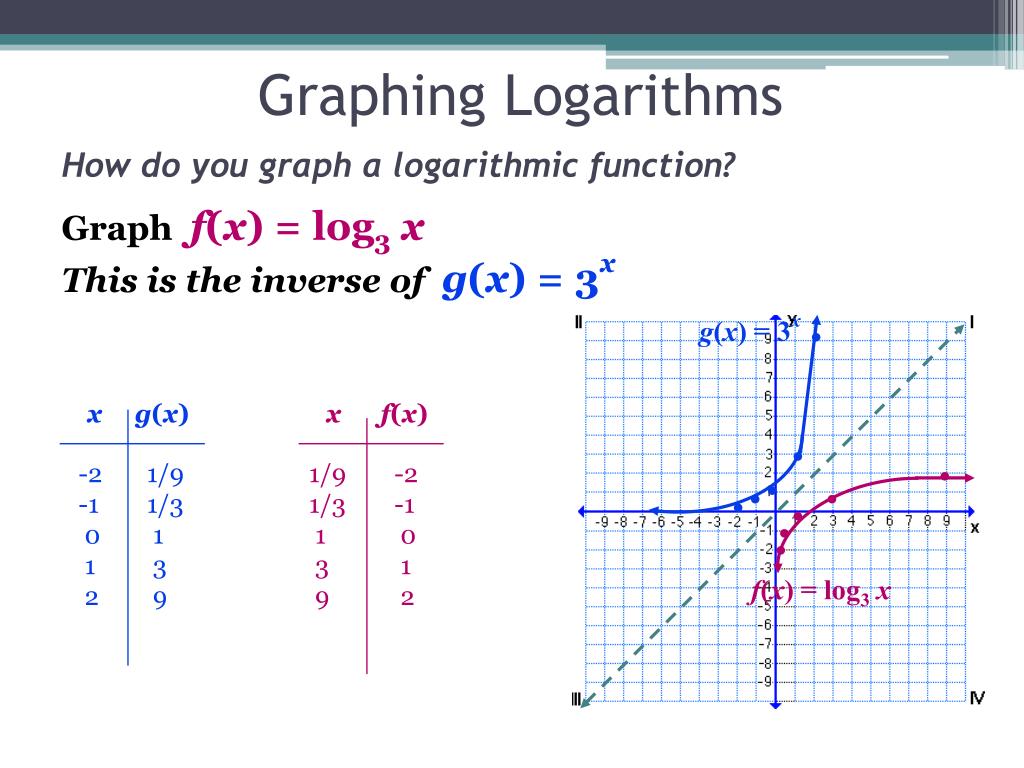
Ppt Graphing Log Functions Powerpoint Presentation Free Download Id

Common Functions Reference

Graph Of A Function Math Examples

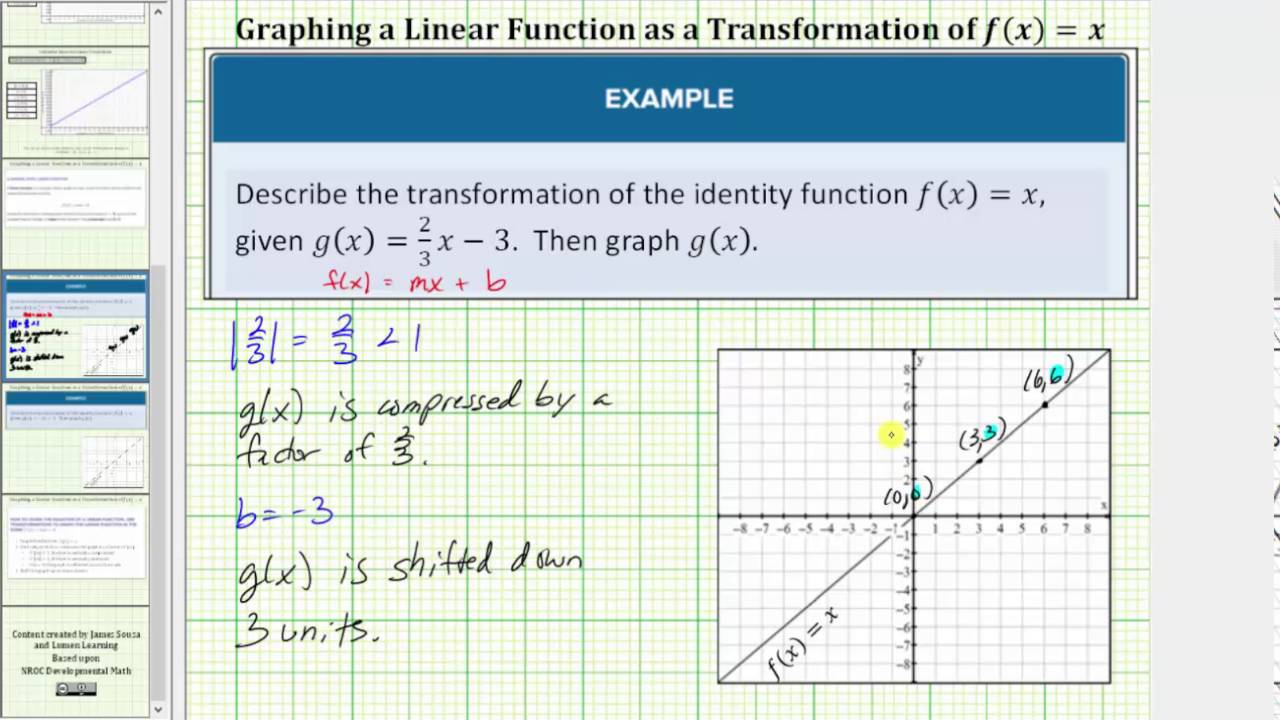
Graph A Linear Function As A Transformation Of F X X Youtube

Functions Maths Gcse Revision

How To Graphically Add Two Functions Mathematics Stack Exchange

Math Scene Equations Iii Lesson 3 Quadratic Equations

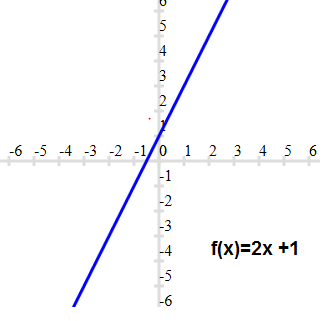
Linear Function Definition Graphs Properties Solved Examples

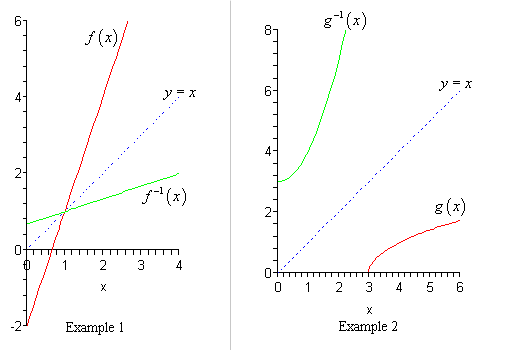
Algebra Inverse Functions

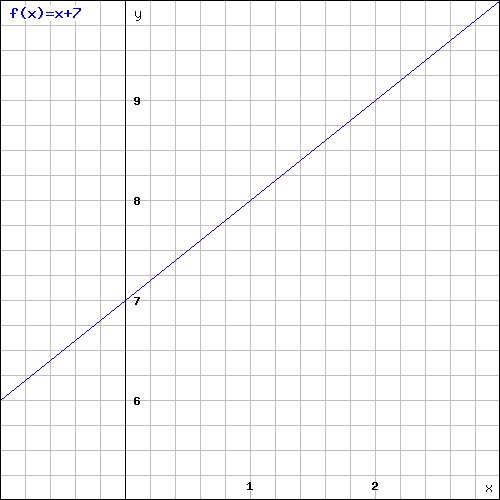
Functions And Linear Equations Algebra 2 How To Graph Functions And Linear Equations Mathplanet

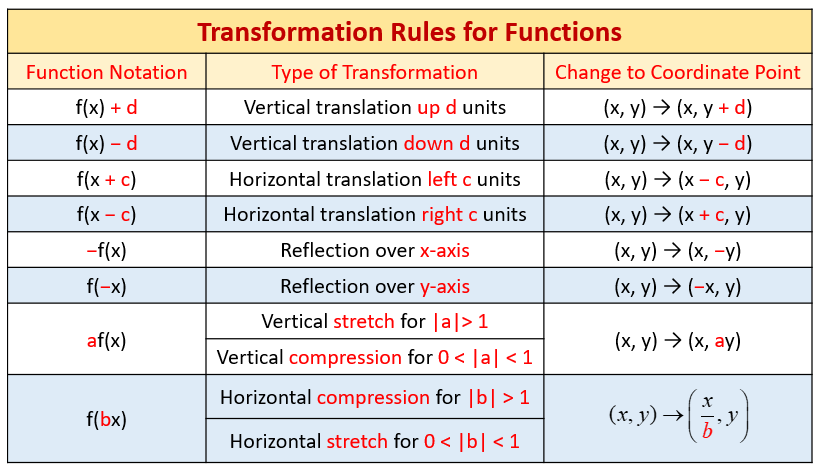
Parent Functions And Their Graphs Video Lessons Examples And Solutions

Function Definition Types Examples Facts Britannica

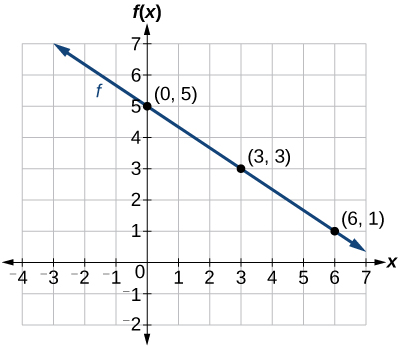
0 2 Graphs Of Linear Functions Mathematics Libretexts

Graphing Quadratic Functions

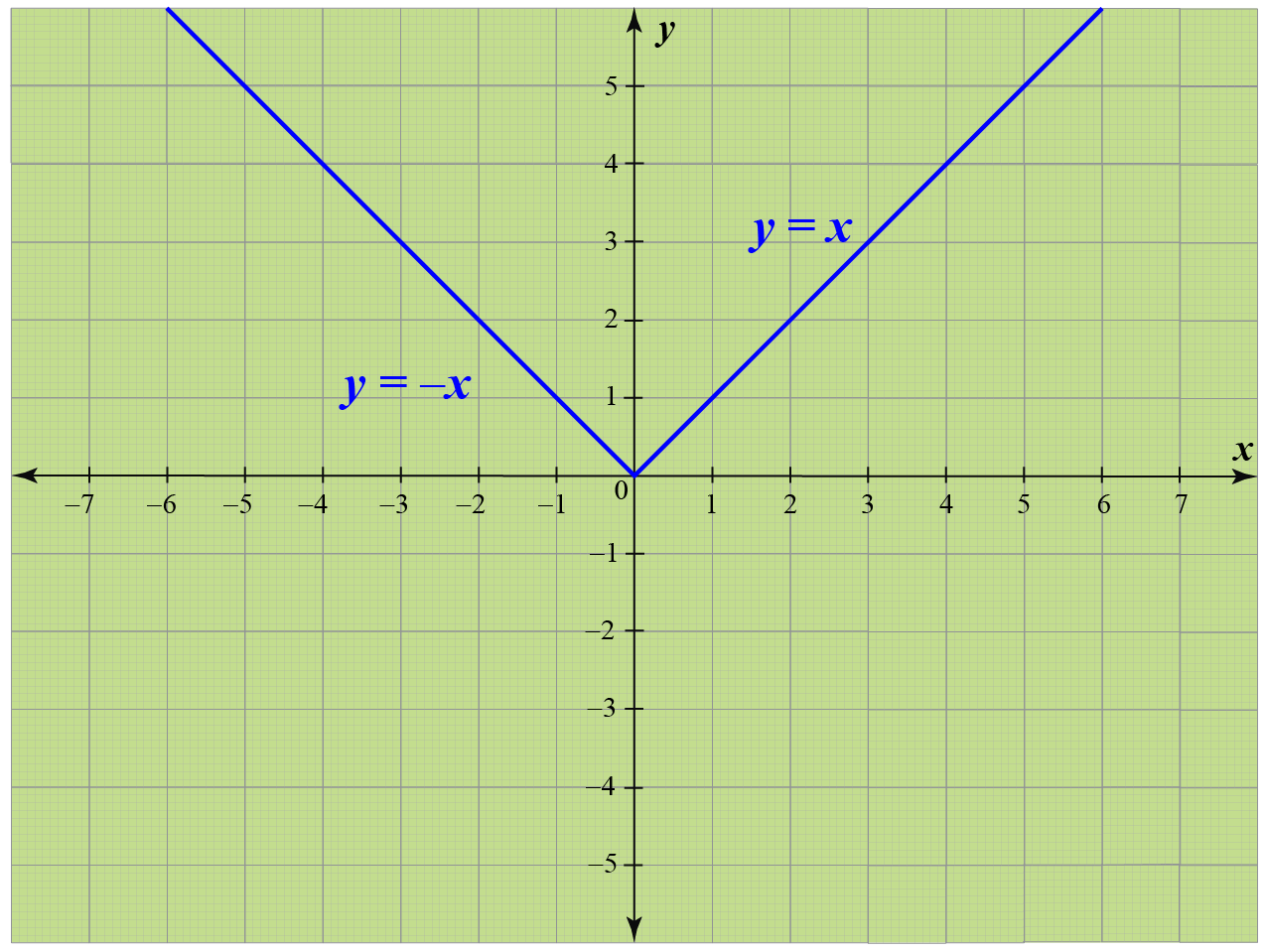
Modulus Function Calculus Graphs Examples Solutions Cuemath

3 Graphs Of Reciprocal Functions Math 4 U

Graphs Types Examples Functions Video Lesson Transcript Study Com

Graph Of A Function Emathzone

Functions And Their Graphs

Notes On Functions And Their Graphs Cbse Class 11 Maths

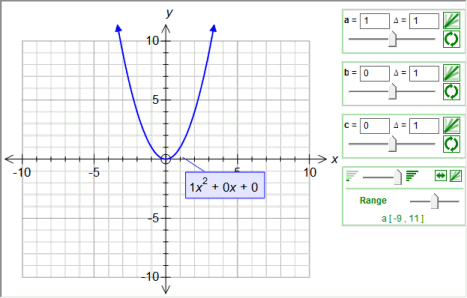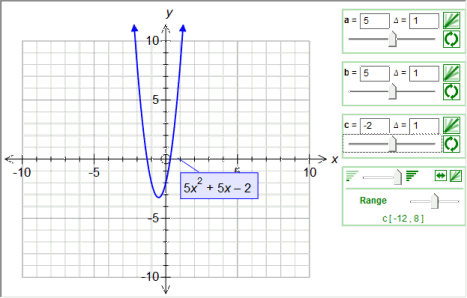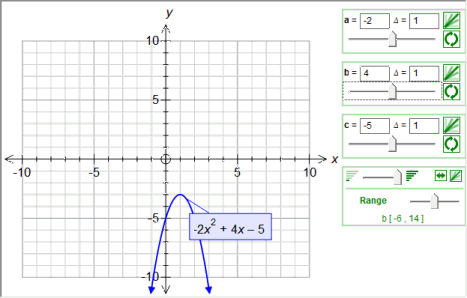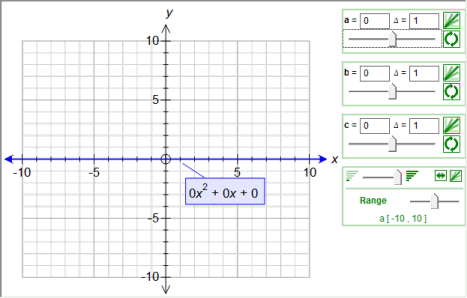
Fx Graph

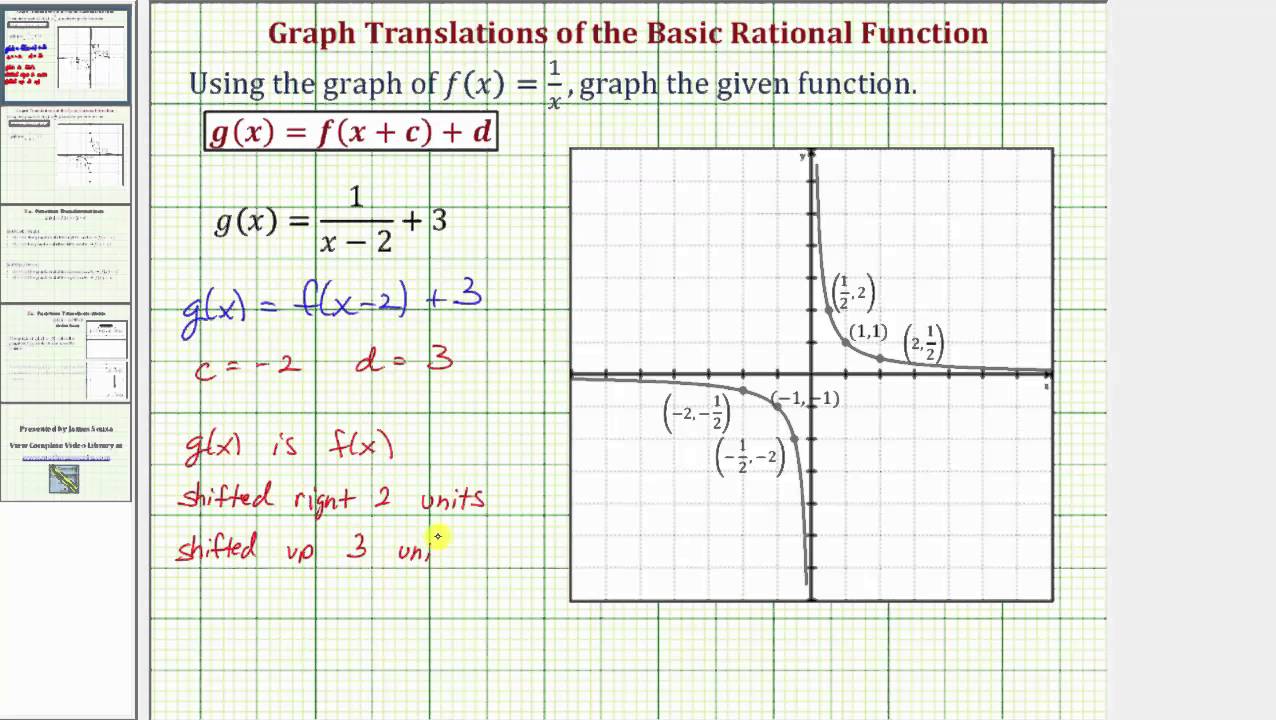
Ex 1 Graph Two Translations Of The Basic Rational Function F X 1 X Youtube

Linear Functions

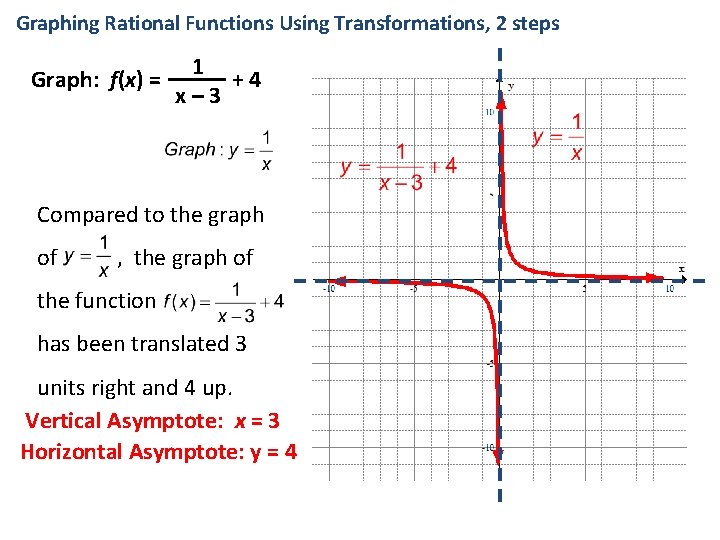
Basic Graph Solving Equations Characteri Stics Rational Functions

Notes Over 5 1 Graphing Exponential Functions Graph Both Functions On The Same Graph Xy Xy A Larger Base Makes It Increase Faster Ppt Download

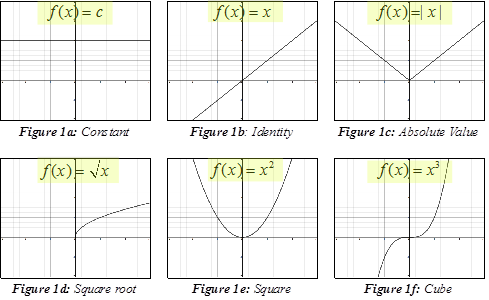
Function Transformations

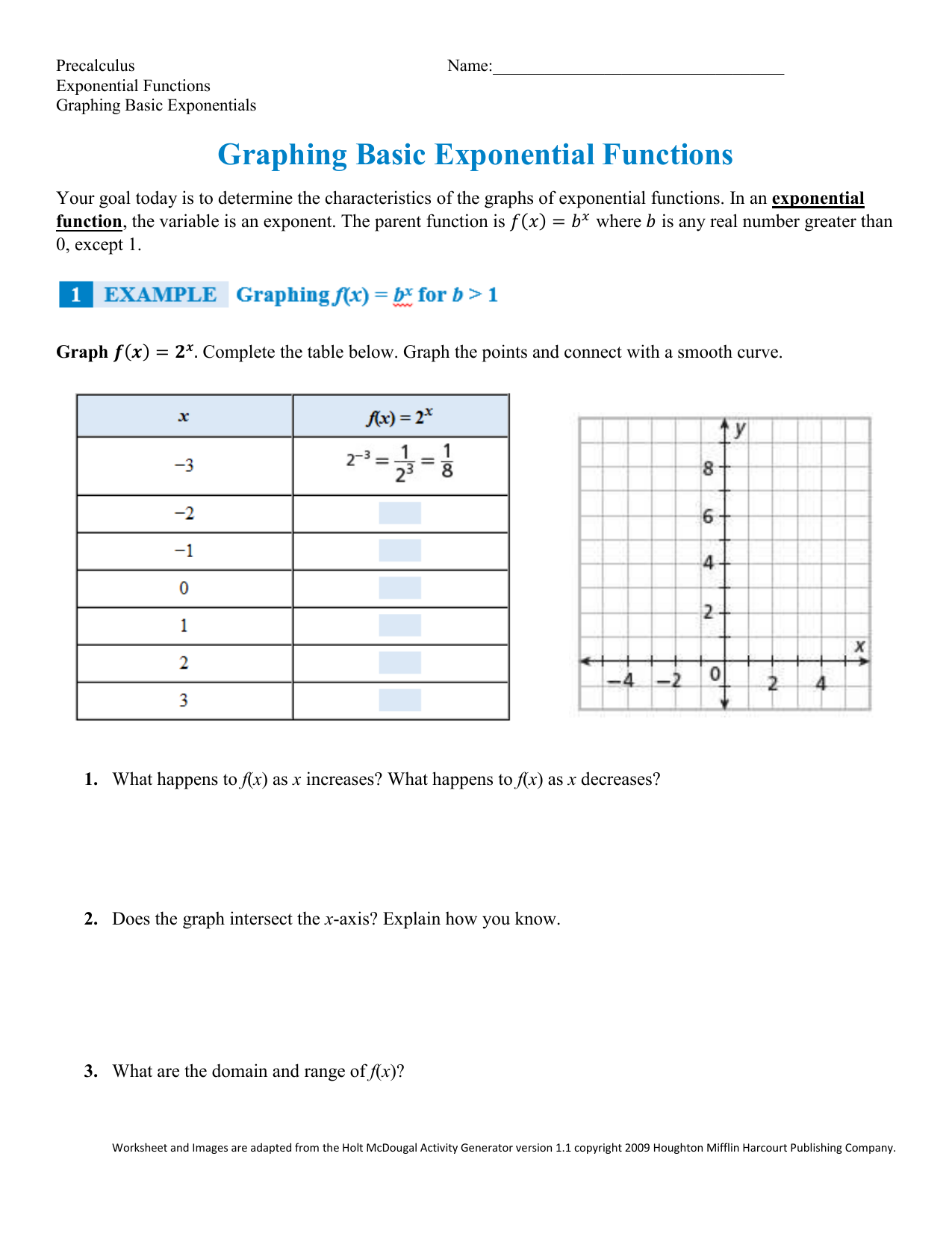
Graph Exponential Functions

Graphs Of Logarithmic Functions Math 126 Precalculus Openstax Cnx

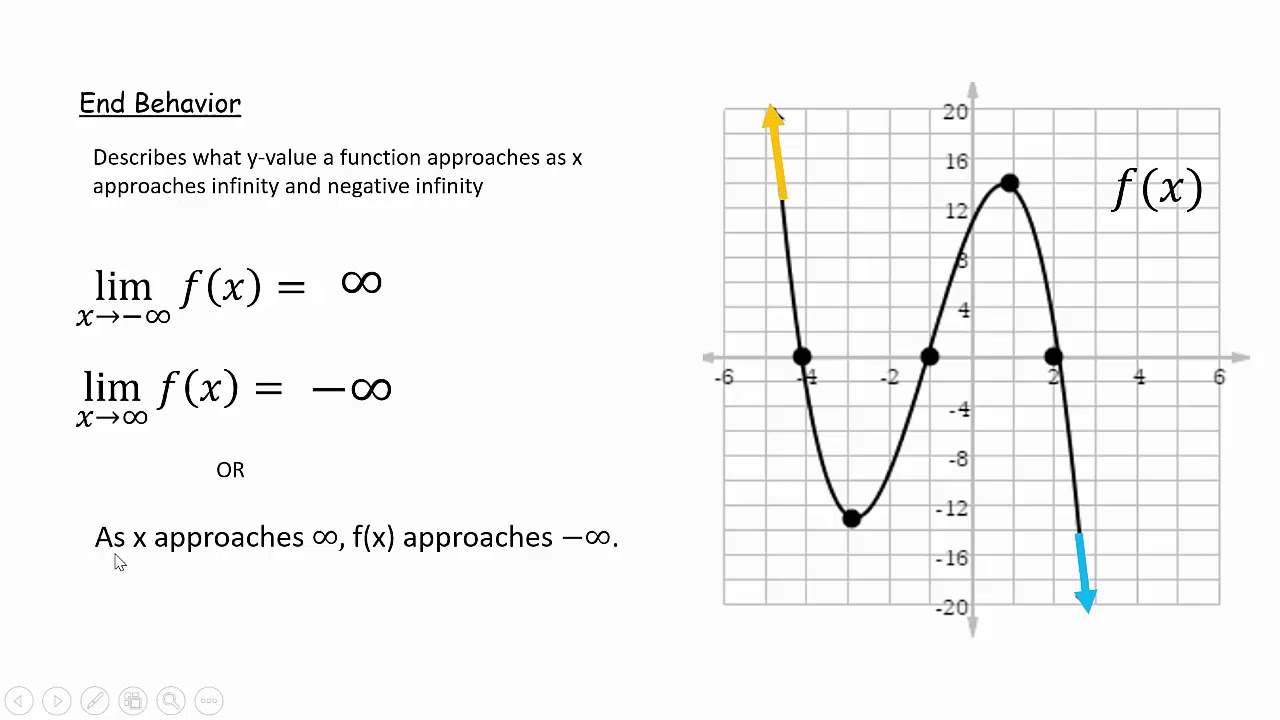
Analyzing Functions From Graphs Youtube

The Graph Shows The Function F X 3x What Is The Value Of X When F X 9 Brainly Com

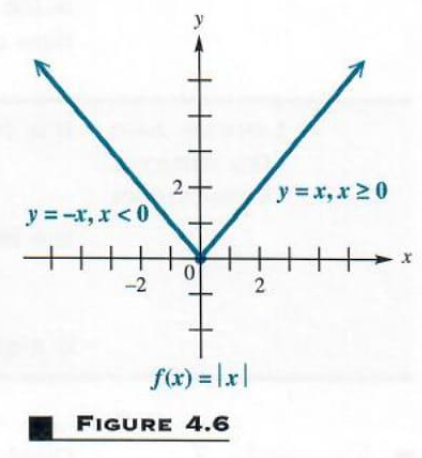
Solve Graphing Basic Functions And Their Step By Step Math Problem Solver

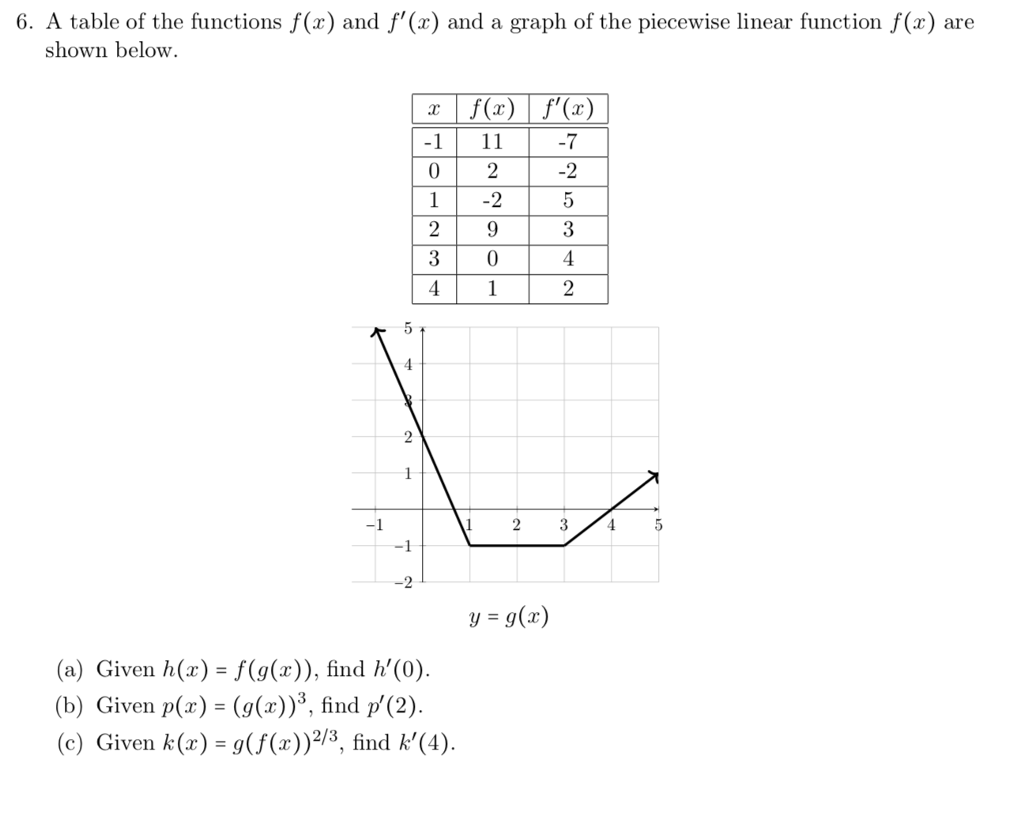
6 A Table Of The Functions F X And F X And A Chegg Com

Understanding F X Function And How To Graph A Simple Function Math Algebra Graphing Functions F If 7 F If 4 Showme

The Graphs Of The Function F X X 2 Is Horizontally Compressed To Obtain Function G Write The Brainly Com

Sketch The Graph Of The Combined Function Of Y G F X For The Following Functions Of F X And G X Mathematics Stack Exchange

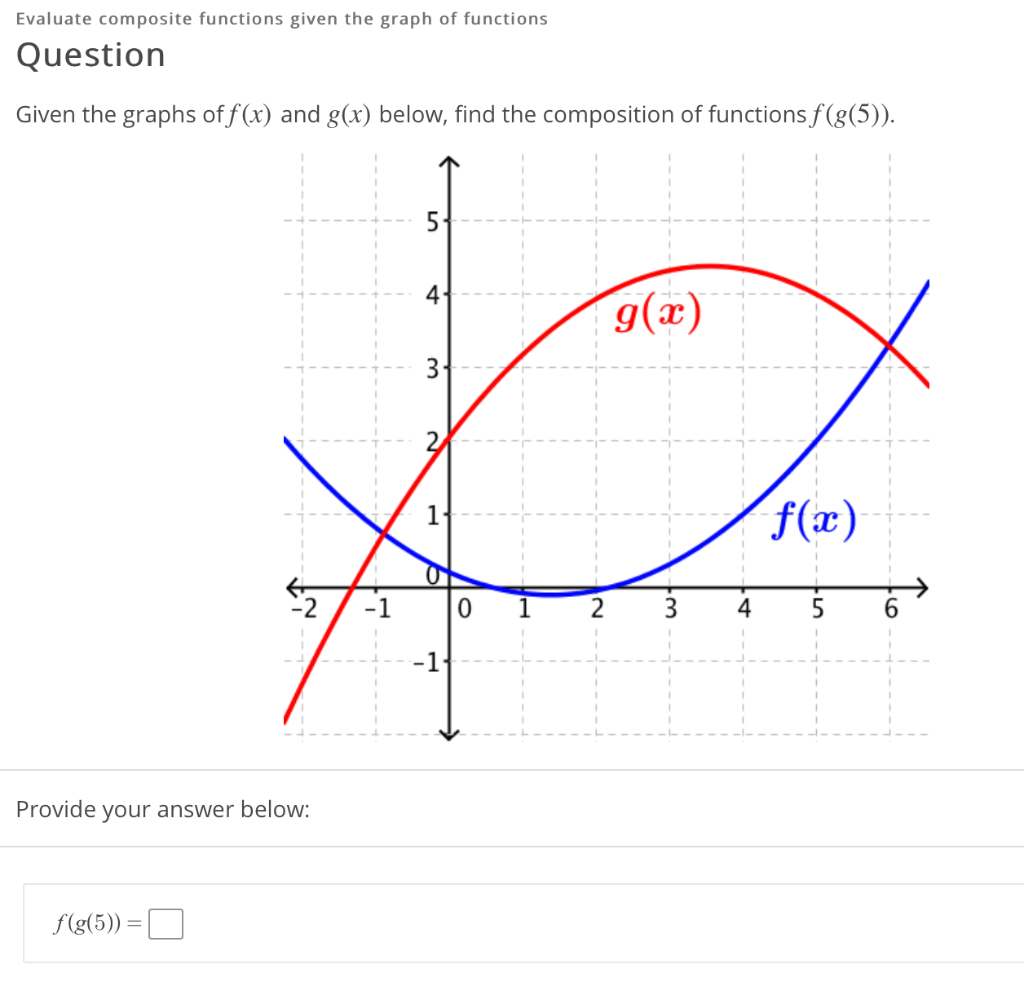
Evaluate Composite Functions Given The Graph Of Chegg Com

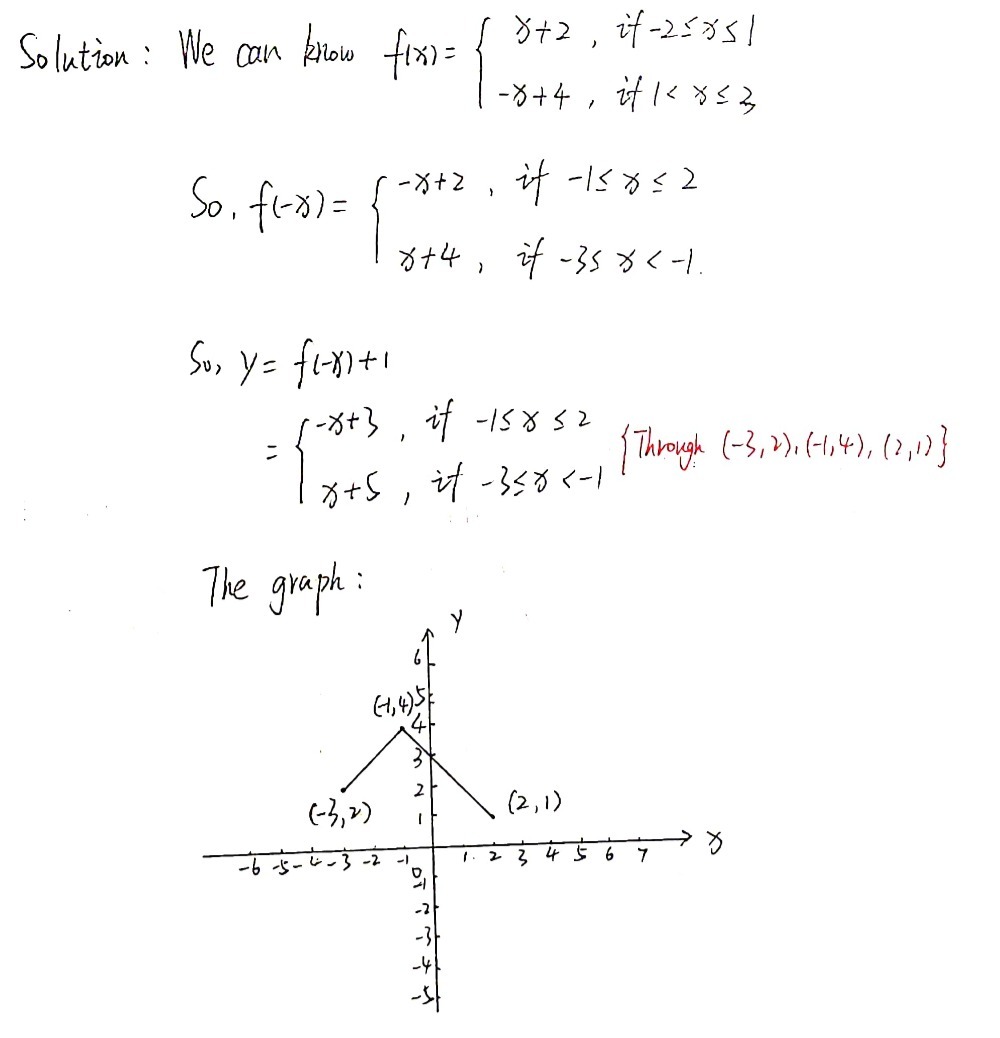
The Graph Of Y Fx Is Given Graph The Indicated Fu Gauthmath

2 Types

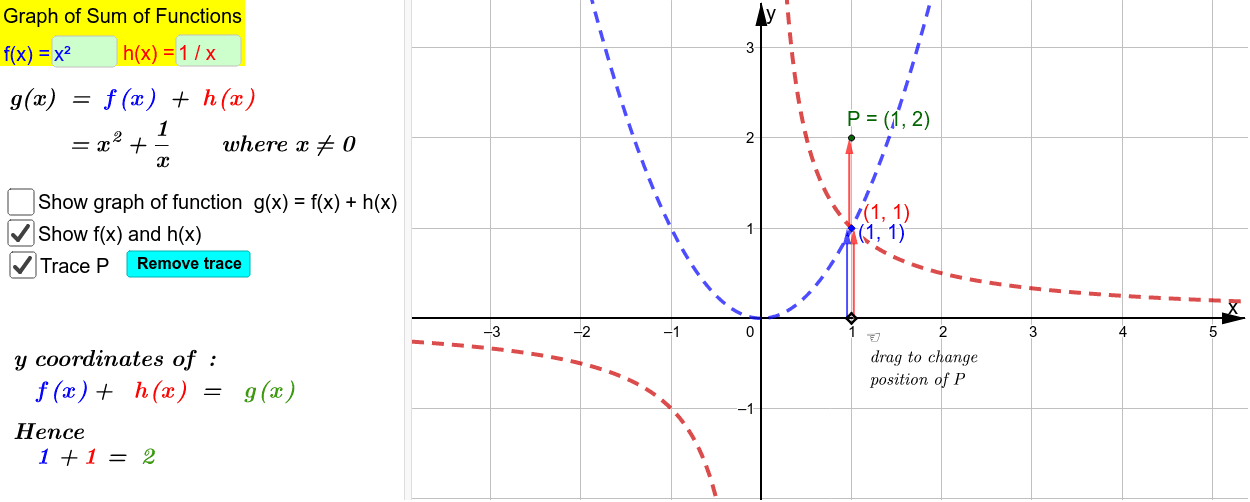
Graph Of Sum Of Two Functions Geogebra

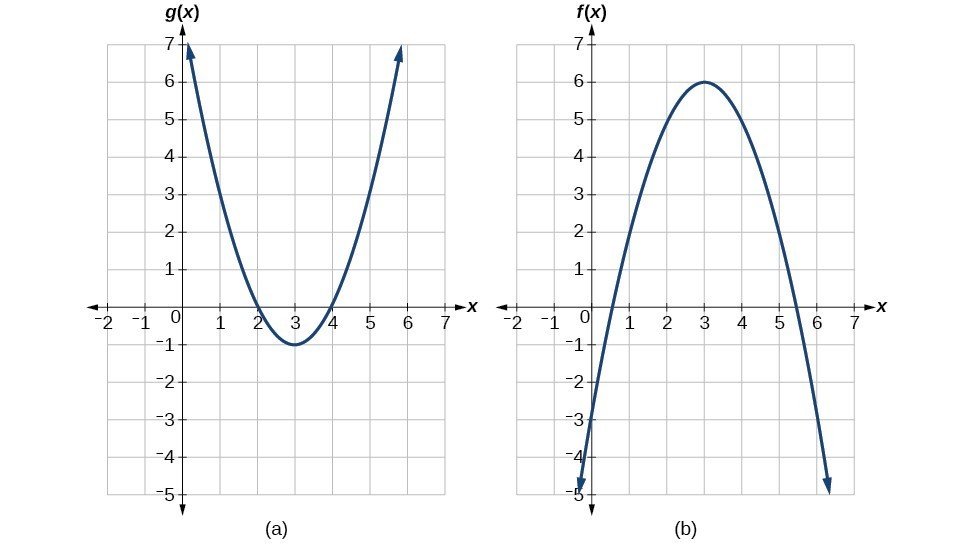
Evaluate Composite Functions College Algebra

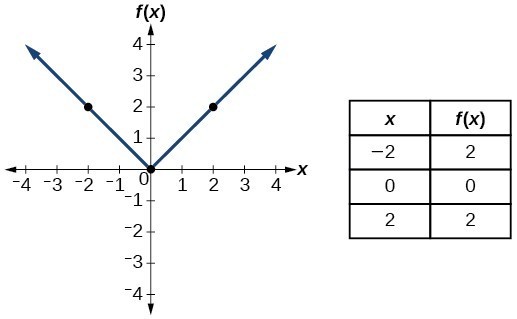
Identify Functions Using Graphs College Algebra

Desmos And Functions Mathematics For Students

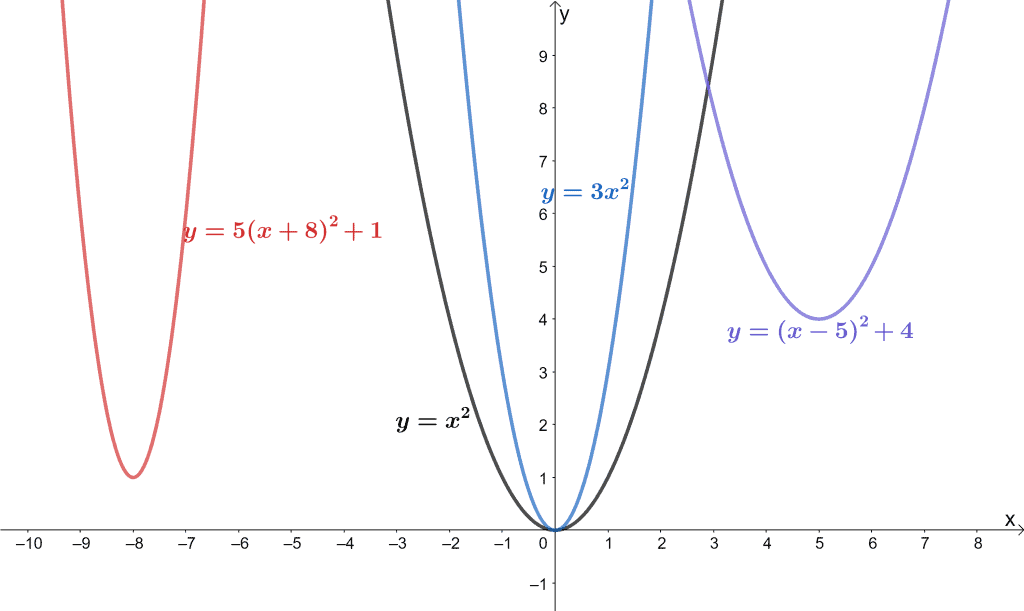
Parent Functions Types Properties Examples

Use The Graph Of A Function To Graph Its Inverse College Algebra

Graphs Of Exponential Functions Read Algebra Ck 12 Foundation

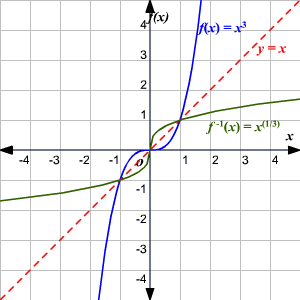
One To One Functions

Given The Graph Of A Function F X Describe Sqrt F X Mathematics Stack Exchange

Evaluating Composite Functions Using Graphs Video Khan Academy

2 2 Functions And Relations Functions Siyavula

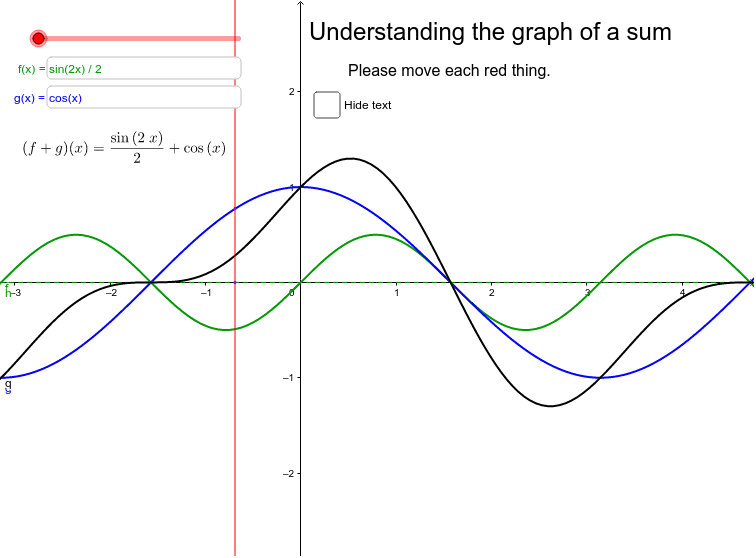
Understanding The Graph Of The Sum Of Two Functions Geogebra

How To Graph Step Functions Video Lesson Transcript Study Com

Graph Of An Equation

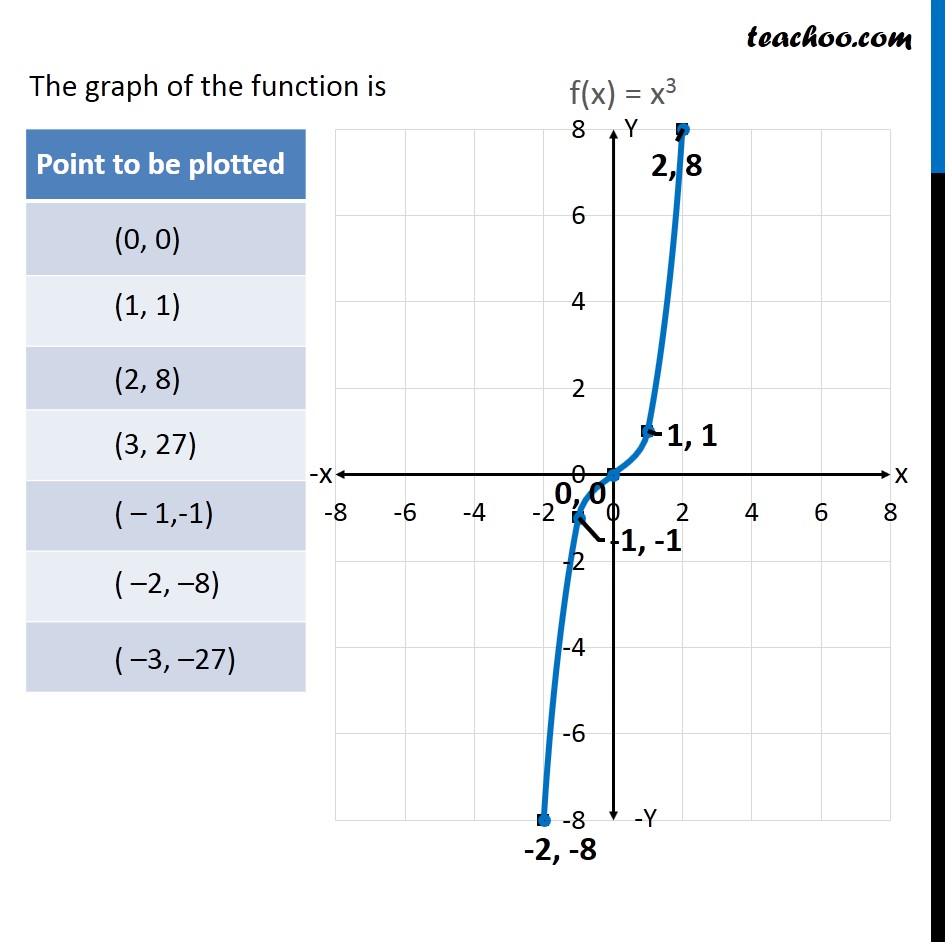
Example 14 Draw Graph Of F X X 3 Chapter 2 Class 11

Sat Math Graph Example 2 Sat Math Forbest Academy

Graphs

Is There A Graphic Visualisation Of F Frac 1 2 Inverse Functions Sat Math Graphing

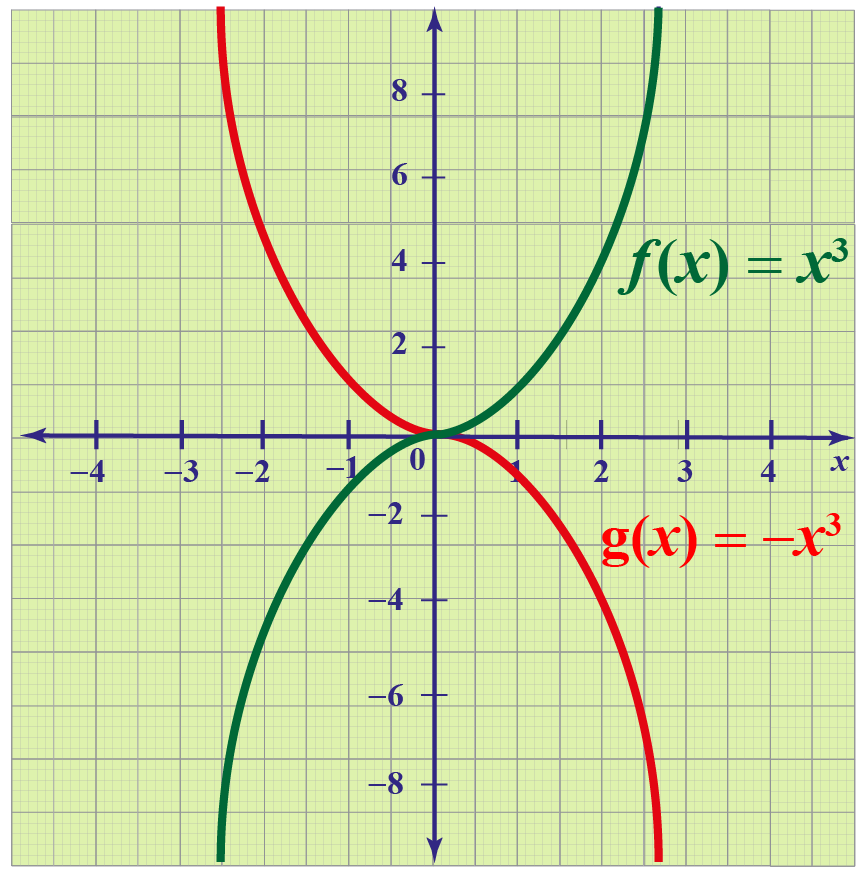
Transformations Of Functions Definitions Facts And Solved Examples Cuemath

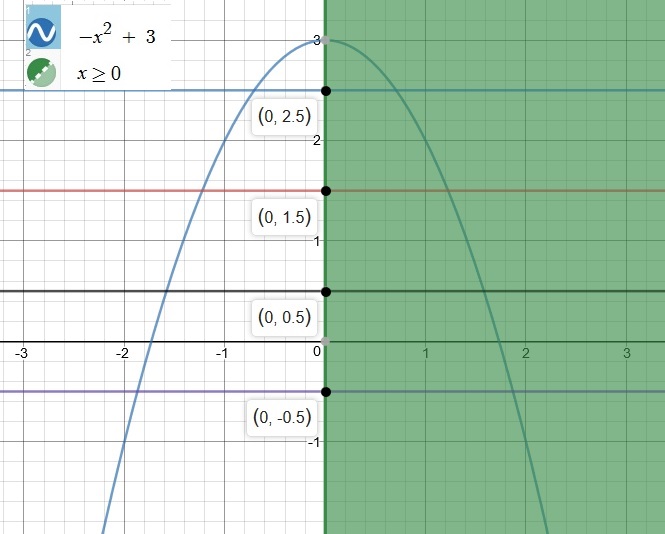
How Do You Graph F X X 2 3 X 0 And Then Use The Horizontal Test To Determine Whether The Inverse Of F Is A Function Socratic

Quadratic Functions And Their Graphs

Efofex Software

Incoming Term: f(x) math graph, f(x) function graph, f(x y) function graph,